
Comment deux mille trente-six divisé par quatre peut-il être égal à dix ?
Et la solution de l’énigme du mois dernier:
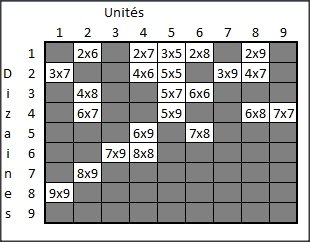

Comment deux mille trente-six divisé par quatre peut-il être égal à dix ?
Et la solution de l’énigme du mois dernier:

Pour ACCEPTER ou REFUSER les conditions détaillées ci-dessous, veuillez faire défiler le texte jusqu’en bas.
Le site internet accessible à l’adresse https://www.la-grange-des-maths.fr/ (ci-après désigné le « Site ») permet à LA GRANGE DES MATHS de présenter à chacun des visiteurs du Site (ci-après désigné le « Visiteur »), les activités et l’actualité de l’association en lui offrant notamment la possibilité de :
Les présentes conditions d’utilisation générales du Site (ci-après désignées les « Conditions d’Utilisation ») ont pour objet d’informer le Visiteur sur les termes et conditions selon lesquels le Visiteur peut accéder au Site et, le cas échéant, utiliser les contenus de toute nature y figurant ou qui y sont attachés (notamment toutes informations, bases de données, données, fichiers, textes, newsletter, images, animations audio et vidéo, interfaces utilisateurs, logos ou toute autre œuvre protégée par le droit d’auteur ou par tout autre droit de propriété).
Toute utilisation ou visualisation du Site suppose que le Visiteur a préalablement accepté de manière expresse les Conditions d’Utilisation qu’il s’engage à respecter. LA GRANGE DES MATHS invite donc tous les Visiteurs à lire attentivement les présentes Conditions d’Utilisation, les imprimer et en conserver une copie.
Pour toute demande d’assistance, plainte, réclamation ou signalement, liés à l’accès ou à l’Utilisation du Site, le Visiteur est invité à contacter LA GRANGE DES MATHS selon les modalités suivantes : par mail à ou par voie postale à l’adresse :Association La Grange des Maths, Espace Charles de Gaulle, 38760 Varces-Allières-et-Risset.
Toute reproduction totale ou partielle des marques figurant sur le Site, sans autorisation expresse et préalable des titulaires de droits est prohibée.
LA GRANGE DES MATHS réalise des traitements de données à caractère personnel dans le cadre du Site. Les informations relatives aux données collectées, aux traitements réalisés, aux droits du Visiteur ainsi qu’aux cookies sont détaillées dans la politique de données à caractère personnel de LA GRANGE DES MATHS : https://www.la-grange-des-maths.fr/politique-de-confidentialite/