Jean, Pierre et Élise ont éclaté un sac de tapioca. Ils sont bien ennuyés car ils n’ont que des feuilles de carton rigide de format A4 (210 x 297 mm) et de l’adhésif pour fabriquer une boîte qui puisse contenir tout le tapioca répandu.
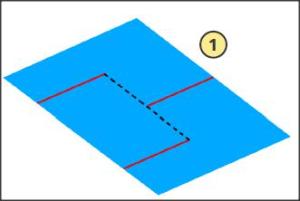
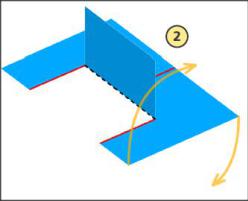
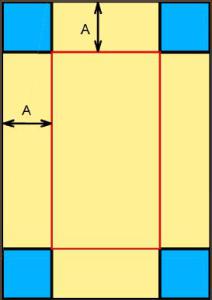
Jean propose de couper les quatre coins, comme sur l’image ci-dessous, de les relever et de les « scotcher ».
Mais quelle hauteur (A) donner à la boîte pour y mettre le maximum de tapioca ?
Élise, qui a bien d’autres préoccupations que les maths, estime que, quelle que soit la hauteur, on aura le même volume.
Pierre, qui aime faire des travaux pratiques, fabrique une première boîte avec A = 25 mm: elle est trop petite. Puis une autre avec A = 60 mm qui est également trop petite. Avec A = 30 mm, c’est mieux mais pas encore tout à fait assez grand. Ses essais sont résumés dans le tableau ci-dessous :
A = 25 mm V = 0,98 litre
A = 30 mm V = 1,06 litre
A = 60 mm V = 0,95 litre.
Mais quel est le volume maximum ?
Pendant ce temps, Jean a calculé ce volume en fonction de la hauteur puis s’est exclamé très fier de lui : « Remplir au maximum… c’est pas ras l’bol !«
Pourquoi Jean est-il si fier de sa formule?
« Plusieurs raisonnements sont possibles, suivant son envie et son niveau en maths :
comme Pierre, on peut faire des essais avec du papier, des ciseaux et du scotch, et trouver petit à petit la meilleure solution.
On peut aussi, comme Jean, trouver la formule donnant le volume de la boîte en fonction de A, et essayer plusieurs valeurs de A pour trouver petit à petit la meilleure solution .
Et si on se souvient des maths du lycée, on peut même déduire du volume de la boîte la formule exacte (un peu compliquée) donnant la meilleure valeur de A.
À vous de jouer… »
Solution de la récré précédente: L’hypercarte
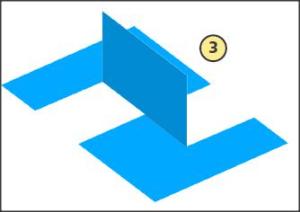
Voici comment découper et plier la feuille pour obtenir la figure 3.