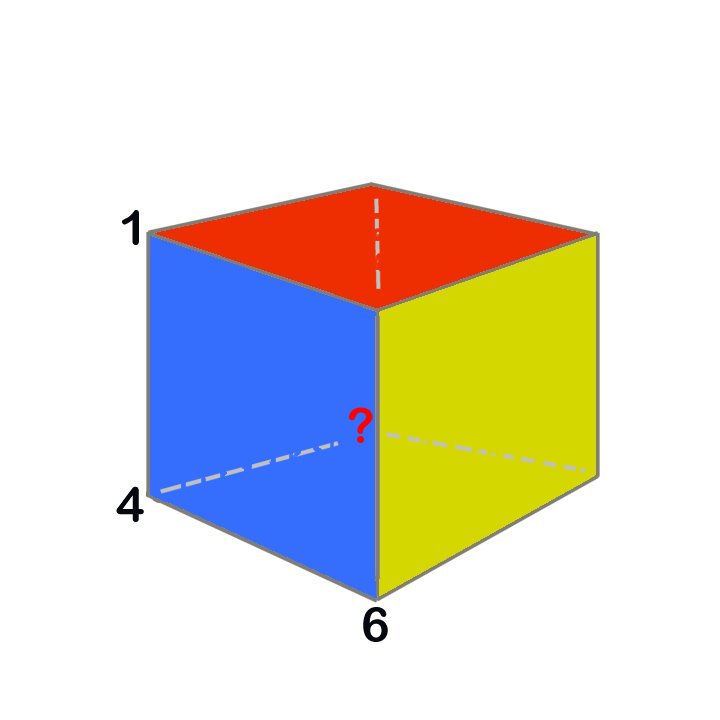
La récré des maths 80: Cube incomplet

Août 4, 2025

Les chiffres 1, 2, 3, 4, 5, 6, 7 et 8 doivent être placés sur les sommets du cube ci dessous. De sorte que la somme des 4 chiffres portés par les 4 sommets de chacune des 6 faces du cube soit la même.

Trouvez le chiffre porté sur le sommet caché de ce cube, (et par suite les autre chiffres manquants)

Et la solution de l’énigme précédente:

Pour obtenir une somme de 13 avec M+C+D+U

M = 2xU et C = 3xD

2U + U + 3D + D = 13,

soit 3U + 4D = 13

D ne peut valoir que 1, 2 ou 3 pour avoir 3xD < 10, mais

on élimine 3 car la somme des chiffres serait 3+9+1+0 et 1 ne peut être le double de 0

2 est également impossible: 6+2, reste 5 non divisible par 3

D=1, et donc 3U = 13 – 4, U=3

le code est 6313

 

En savoir plus sur La grange des maths

Abonnez-vous pour poursuivre la lecture et avoir accès à l’ensemble des archives.

Poursuivre la lecture

Conditions générales d’utilisation

Pour ACCEPTER ou REFUSER les conditions détaillées ci-dessous, veuillez faire défiler le texte jusqu’en bas.

1. SITE INTERNET

Le site internet accessible à l’adresse https://www.la-grange-des-maths.fr/ (ci-après désigné le « Site ») permet à LA GRANGE DES MATHS de présenter à chacun des visiteurs du Site (ci-après désigné le « Visiteur »), les activités et l’actualité de l’association en lui offrant notamment la possibilité de :

  • recevoir la lettre d’information du Site (newsletter) en communiquant son adresse électronique ;
  • télécharger un formulaire d’adhésion à LA GRANGE DES MATHS ;
  • télécharger une fiche de don à LA GRANGE DES MATHS ;
  • effectuer une réservation de valise pédagogique au moyen d’un formulaire de réservation.

 

2. OBJET

Les présentes conditions d’utilisation générales du Site (ci-après désignées les « Conditions d’Utilisation ») ont pour objet d’informer le Visiteur sur les termes et conditions selon lesquels le Visiteur peut accéder au Site et, le cas échéant, utiliser les contenus de toute nature y figurant ou qui y sont attachés (notamment toutes informations, bases de données, données, fichiers, textes, newsletter, images, animations audio et vidéo, interfaces utilisateurs, logos ou toute autre œuvre protégée par le droit d’auteur ou par tout autre droit de propriété).

 

3. ACCEPTATION DES CONDITIONS D’UTILISATION

Toute utilisation ou visualisation du Site suppose que le Visiteur a préalablement accepté de manière expresse les Conditions d’Utilisation qu’il s’engage à respecter. LA GRANGE DES MATHS invite donc tous les Visiteurs à lire attentivement les présentes Conditions d’Utilisation, les imprimer et en conserver une copie.

 

4. ACCÈS AUX CONTENUS DU SITE

    • Le Visiteur peut consulter librement, pour son usage privé et non commercial, les informations qui figurent sur le Site, sous réserve du respect des Conditions d’Utilisation en ce compris du respect des droits de propriété intellectuelle tels que définis ci-après.
    • L’Accès au Site et à ses fonctionnalités est gratuit. Le Visiteur conserve à sa charge exclusive les frais afférents aux équipements et à l’établissement de la connexion Internet nécessaires pour accéder au Site et en utiliser les fonctionnalités ainsi que les frais téléphoniques résultant des appels dont il est à l’origine en lien avec l’accès ou l’utilisation du Site.
    • LA GRANGE DES MATHS s’efforce au mieux de fournir sur le Site des informations exactes et précises. LA GRANGE DES MATHS met à jour régulièrement ces informations selon sa convenance. Ces informations sont néanmoins fournies à titre indicatif et ne revêtent aucun caractère contractuel. Les informations qui figurent sur le Site sont mises à jour régulièrement par LA GRANGE DES MATHS à sa convenance.
    • Malgré tous les soins apportés pour la constitution et la mise à jour du Site, des erreurs, inexactitudes ou omissions peuvent subsister ainsi que des problèmes de connexion au Site ou d’interruption dans la connexion. LA GRANGE DES MATHS décline toute responsabilité à cet égard.

 

5. NEWSLETTER

    • L’abonnement à la lettre d’information (newsletter) du Site nécessite la saisie d’une adresse électronique par le Visiteur (ci-après l’ « Abonné»).
    • L’Abonné est seul garant de l’actualité et de la véracité de l’adresse électronique fournie à LA GRANGE DES MATHS. En conséquence, l’Abonné s’engage à vérifier et à mettre à jour régulièrement son adresse électronique.
    • L’Abonné a la possibilité de se désinscrire de la newsletter en envoyant simplement un email à l’adresse suivante :

 

6. COMPORTEMENT ET OBLIGATIONS DU VISITEUR

    • Le Visiteur, qu’il soit simple Visiteur ou également Abonné, s’engage à utiliser le Site et les fonctionnalités qui y sont proposées en se comportant de manière responsable, courtoise ainsi que dans le respect des règles en vigueur et s’engage notamment à :
  • ne pas se livrer sur le Site à une quelconque activité illicite en ce compris de manière non exhaustive la communication au travers du Site de contenu illégal, injurieux, diffamatoire, d’incitation à la haine raciale, d’apologie du terrorisme ou de tout contenu contraire aux bonnes mœurs ;
  • ne pas se livrer sur le Site à une quelconque activité de nature à causer un préjudice à des tiers en ce compris de manière non exhaustive ne pas porter atteinte au travers du Site au droit à la vie privée, au droit à l’image, aux droits de propriété intellectuelle ou autres droits de propriété dont des tiers seraient titulaires ;
  • ne pas mettre en péril l’intégrité et/ou le bon fonctionnement du Site et/ou de l’une de ses fonctionnalités en ce compris de manière non exhaustive ne pas chercher à violer les mesures de sécurité mises en place sur le Site, ne pas exposer le Site à un virus, ne pas porter atteinte ou chercher à limiter ou à détruire le fonctionnement du Site et/ou de l’une de ses fonctionnalités, ne pas créer une surcharge sur les serveurs du Site ;
  • garantir la licéité, la complétude, l’exactitude des informations et données qu’il peut être amené à fournir à LA GRANGE DES MATHS ;
  • assumer l’ensemble des risques et responsabilités afférent à l’accès et à l’utilisation du Site et de ses fonctionnalités qui doivent rester sous son entier contrôle.
    • En cas de violation par le Visiteur de l’une quelconque des Conditions d’Utilisation, LA GRANGE DES MATHS se réserve le droit d’engager à l’encontre du Visiteur tout recours visant à engager sa responsabilité ainsi que de prendre toute mesure permettant de faire cesser cette violation.

 

7. CONTACT

Pour toute demande d’assistance, plainte, réclamation ou signalement, liés à l’accès ou à l’Utilisation du Site, le Visiteur est invité à contacter LA GRANGE DES MATHS selon les modalités suivantes : par mail à ou par voie postale à l’adresse :Association La Grange des Maths, Espace Charles de Gaulle, 38760 Varces-Allières-et-Risset.

8. PROPRIÉTÉ INTELLECTUELLE

    • Dispositions générales
      • Le Site et son contenu sont protégés par des droits de propriété intellectuelle. Sauf mention contraire, toutes les informations et documents qui figurent sur le Site ainsi que tous les éléments créés pour le Site sont la propriété de LA GRANGE DES MATHS et sont protégés par des droits de propriété intellectuelle. La structure générale, les logos ainsi que les textes, les images, photographies, vidéos, et autres contenus sont la propriété de LA GRANGE DES MATHSou de ses fournisseurs de contenus ou partenaires et sont soumis aux dispositions du Code de la propriété intellectuelle.
      • Aucune disposition des Conditions d’Utilisation ne peut être interprétée comme opérant une cession, une vente, une transmission ou une mise à disposition de quelque manière que ce soit des droits de propriété intellectuelle dont LA GRANGE DES MATHS, ses fournisseurs de contenus ou ses partenaires sont titulaires au profit du Visiteur. Aucune licence, ni aucun droit autre que celui de consulter le site, n’est conféré au Visiteur au regard des droits de propriété intellectuelle dont LA GRANGE DES MATHS est titulaire.
    • Marques

Toute reproduction totale ou partielle des marques figurant sur le Site, sans autorisation expresse et préalable des titulaires de droits est prohibée.

  • Base de données
    • Conformément aux dispositions des articles L341-1 et suivants du Code de la propriété intellectuelle, LA GRANGE DES MATHS est producteur et propriétaire de tout ou partie des bases de données composant le Site.
    • Toute opération visant à extraire, réutiliser, stocker, reproduire, représenter ou conserver, directement ou indirectement, par transfert permanent ou temporaire, sur un support quelconque, par tout moyen et sous toute forme que ce soit, y compris par lien(s) hypertexte(s), tout ou partie qualitativement ou quantitativement substantielle du contenu des bases de données figurant sur le Site ainsi que toute opération visant à faire l’extraction ou la réutilisation répétée et systématique de parties qualitativement et quantitativement non substantielles lorsque ces opérations excèdent manifestement les conditions d’utilisation normale est donc prohibée.
  • Liens hypertexte
    • Des liens hypertexte renvoyant vers des sites internet ou autres sources externes qui ne sont pas gérés par LA GRANGE DES MATHS peuvent figurer sur le Site. Ces éventuels liens sont proposés au Visiteur par LA GRANGE DES MATHS à titre de service. La décision d’activer les liens appartient exclusivement au Visiteur. LA GRANGE DES MATHS ne pourra être tenue responsable de la mise à disposition de ces sites et autres sources externes au travers du Site et décline toute responsabilité quant à leur contenu ou aux contenus auxquels ces derniers renvoient.
    • Toute création d’un lien hypertexte simple et/ou profond renvoyant vers le Site ou utilisation de la technique dite de « framing » sans le consentement préalable et express de LA GRANGE DES MATHS est illicite. En conséquence, aucun élément figurant sur une page du Site ne peut être partiellement ou totalement diffusé, transféré ou inséré sur un autre site Internet, ni servir à créer des produits dérivés, sauf autorisation expresse de LA GRANGE DES MATHS. Tout lien simple ou profond et/ou  » framing  » devra faire l’objet d’une autorisation expresse, préalable et écrite de LA GRANGE DES MATHS.
  • Respect des droits de propriété intellectuelle par le Visiteur
    • Le Visiteur s’engage à respecter les droits de propriété intellectuelle dont LA GRANGE DES MATHS, ses fournisseurs de contenus et ses partenaires sont titulaires et s’interdit d’en faire un usage quelconque.
    • À l’exception de la reproduction et de l’utilisation de tous documents et informations publiés sur le Site à des fins exclusivement d’information pour un usage strictement personnel et privé et moyennant mention de la source, toute reproduction ou représentation totale ou partielle du Site faite sans le consentement préalable et express de LA GRANGE DES MATHS est illicite. Pour toute demande relative à l’utilisation ou la reproduction de contenus ou documents issus du Site, merci de vous adresser par courrier à : La Grange des Maths, Espace Charles de Gaulle, 38760 Varces-Allières-et-Risset.
    • À l’exception de l’utilisation strictement personnelle et privée par le Visiteur de la structure du Site et de ses éléments logiciels, l’utilisation de la structure du Site et de ses éléments logiciels mettant notamment en œuvre tout ou partie des bases de données du Site pour une utilisation des fins professionnelles et/ou commerciales est prohibée.
    • Toute violation des dispositions du présent article est susceptible d’engager la responsabilité du Visiteur, notamment civile et pénale, pour actes de contrefaçon, concurrence déloyale et/ou de parasitisme et exposera celui-ci à des poursuites judiciaires. LA GRANGE DES MATHS, ses fournisseurs de contenus et ses partenaires se réservent également le droit de prendre toute mesure d’urgence pour faire cesser l’atteinte ainsi portée à leurs droits.

9. DONNÉES À CARACTÈRE PERSONNEL ET COOKIES

LA GRANGE DES MATHS réalise des traitements de données à caractère personnel dans le cadre du Site. Les informations relatives aux données collectées, aux traitements réalisés, aux droits du Visiteur ainsi qu’aux cookies sont détaillées dans la politique de données à caractère personnel de LA GRANGE DES MATHS : https://www.la-grange-des-maths.fr/politique-de-confidentialite/

10. LIMITATIONS DE RESPONSABILITÉ

    • LA GRANGE DES MATHS fournit ses meilleurs efforts pour assurer le bon fonctionnement et la sécurité du Site et de ses fonctionnalités ainsi que l’exactitude et la mise à jour des informations qui y figurent. Toutefois, malgré tous les soins apportés à la réalisation de ce Site et à son actualisation régulière, le Site est susceptible de contenir des inexactitudes et/ou des erreurs dans les informations qu’il contient. Des changements et mises à jour sont régulièrement effectués sur le Site par LA GRANGE DES MATHS qui ne saurait être tenue responsable de la qualité, l’exactitude, l’actualité, l’ordre ou l’exhaustivité des données figurant sur le Site ni tenue à aucune obligation de mise à jour des informations.
    • LA GRANGE DES MATHS exclut toute garantie quelle qu’elle soit quant :
  • au contenu du Site et à l’ensemble des informations accessibles sur et depuis le Site. En aucun cas, LA GRANGE DES MATHS(ou tout tiers impliqué dans la création ou le fonctionnement du Site) ne saurait être tenue pour responsable ou redevable vis-à-vis d’un Visiteur ou de tout autre tiers, des dommages directs ou indirects, découlant de l’utilisation du Site, de l’utilisation des informations diffusées sur le Site et/ou de l’utilisation d’un produit auquel ces informations font référence. Il appartient au Visiteur de vérifier la précision des informations fournies ;
  • aux dysfonctionnements, incompatibilités, défaut de sécurité, problème de configuration ou de mise à jour liés à l’équipement personnel du Visiteur ou liés à son navigateur et impactant son accès ou son utilisation du Site ou de l’une de ses fonctionnalités ;
  • aux dysfonctionnements imputables aux fournisseurs d’accès, aux temps de transfert des documents ou informations ;
  • aux dysfonctionnements ou interruption de l’accès au Site ou à l’une de ses fonctionnalités dus à un évènement de force majeure au sens de la loi et de la jurisprudence ;
  • à l’interruption provisoire du fonctionnement du Site consécutive à une action de LA GRANGE DES MATHS pour améliorer le Site ou l’une de ses fonctionnalités ou à l’occasion d’opérations de maintenance (programmées ou d’urgence) que LA GRANGE DES MATHS pourra être amenée à mettre en œuvre de façon occasionnelle et sans préavis. LA GRANGE DES MATHS ne pourra être tenue responsable de tout dommage causé par de telles opérations de mise à jour ou de maintenance.

 

11. MODIFICATION DU SITE ET DES CONDITIONS D’UTILISATION

    • Le Site est évolutif et LA GRANGE DES MATHS peut être amenée à en modifier notamment le contenu, les fonctionnalités ou la localisation à sa seule discrétion, unilatéralement, à tout moment et sans préavis.
    • LA GRANGE DES MATHS se réserve le droit de modifier ou de corriger le contenu du Site ainsi que sa configuration. LA GRANGE DES MATHS se réserve aussi le droit, sous les mêmes conditions, d’éliminer, de modifier ou de corriger les services ou le contenu du Site, d’en limiter, suspendre ou interdire l’accès, de façon provisoire ou définitive.
    • LA GRANGE DES MATHS peut être amenée à modifier les Conditions d’Utilisation, et ce en tout ou partie et à tout moment. Les Visiteurs seront informés de ces modifications par la mise en ligne sur le Site d’un bandeau informatif les invitant à consulter les Conditions d’Utilisation modifiées avant de les accepter.
    • Au cas où une clause ou condition des Conditions d’Utilisation serait reconnue en tout ou partie nulle ou illicite, elle sera réputée non écrite, sans que la validité des autres clauses ou conditions des Conditions d’Utilisation en soit affectée.
    • La dernière mise à jour des Conditions d’Utilisation date du 6/6/2021.