Un grand-père choisi 5 billets de valeurs différentes, celui de 5, celui de 10, de 20, de 50 et celui de 100 euros.
Il met discrètement chacun de ces billets dans 5 enveloppes (un seul billet par enveloppe).
Ce grand-père demande alors à chacun de ses petits-enfants Adrien, Benoît, Carl et Didier de choisir au hasard une des enveloppes et de regarder discrètement son contenu et d’annoncer.
Adrien : » Aucun de mes frères n’a un billet de plus que 50 € et Benoît a eu moins de 50 €. »
Benoît : » Le mien est de 100 € et celui d’Adrien est de 10 €. »
Carl : » Le mien dépasse celui de 10 et celui de Didier a une valeur plus grande que celle d’Adrien. »
Didier : » J’ai eu moins de 5 € et Benoît a eu plus que Carl. »
Alors le Grand-père s’exclame: » Vilains petits menteurs ! un seul parmi vous a dit la vérité »
, les autres ont menti sur toute leur déclaration.
Qui a dit la vérité ?
Quelle est la part de chacun ?
Attention il y a 2 solutions possibles

Et la solution de l’énigme précédente:
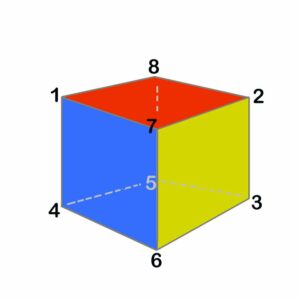
Le cube ayant 6 faces, comme chaque chiffre est présent sur 3 faces, additionner 3 fois la somme des entiers revient à additionner 6 fois la somme constante pour chaque face.
La somme des 8 chiffres = 36, 3 x 36 = 108, donc chaque face a une somme = 108 / 3 = 18
on déduit les faces visibles :
1 4 6 7,
6 7 2 3
1 8 2 7
Donc le sommet caché porte le chiffre 5
donnant les faces:
1 8 5 4
5 8 2 3
et 4 5 3 6